머신러닝의 수 많은 알고리즘은 고차원의 공간에 벡터 형식으로 정보를 저장하곤 하는데, 수 백 천 만 되가는 차원을 그대로 이해하기엔 인간의 뇌는 버겁다. 그래서 이를 해결하려고 고차원 공간을 2차원으로 압축하고 시각화 할 수 있는 임베딩 방법들이 이용되고는 한다. 임베딩 방법은 현재도 많이 연구되고 있으며, 제목에 적혀있듯 t-SNE, PCA, LLE, MDS 이 네 가지 방법을 살펴보도록 하려고 합니다.
우선 간단하게 각 임베딩 방법을 설명하자면
t-SNE: t-Stochastic Neighbor Embedding, t-분포 확률적 임베딩, 2008년에 제안된 방법이며 Student 라는 가명의 학자가 발표한 t-분포에서 이름을 따왔다고 한다.
t-SNE는 고차원의 벡터로 표현되는 데이터 간의 neighbor structure를 보존하는 2차원의 embedding vector를 학습함으로써 고차원의 데이터를 2차원의 지도로 표현한다.
t-SNE는 벡터 시각화를 위한 다른 알고리즘들보다 안정적인 임베딩 학습 결과를 보여즌다.
이는 t-SNE가 데이터 간 거리를 stochastic probability로 변환하여 임베딩에 이용하기 때문이다.
그리고 이 stochastic probability는 perplexiy에 의하여 조절 된다.
PCA: Princial Component Analysis, 주성분 분석이라고 하며 변수가 너무 많아 기존 변수를 조합해 새로운 변수를 가지고 모델링을 하려고 할 때 주로 PCA를 사용한다.
원래 제대로 이해하려면 선형대수학 관련 이해가 필요하지만 여기서는 간단하게만 설명하고 넘기려고 한다.
훈련 데이터의 모든 특성(feature)이 결과에 주요한 영향을 끼치는 것은 아니다.
가장 중요한 특성이 있을 것이고, 쓸모없는 특성도 있을 건데, 모든 특성 중 몇 개의 특성만 선택하는 게 PCA입니다.
쓸모 없는 특성이 제거되면서 노이즈 제거, 메모리 절약, 모델 성능 향상 등의 효과를 보여준다.
LLE: Locally Linear Embedding, 비선형 차원 축소라고 하며, 원 공간에서의 최인접 이웃의 정보 locality에 집중하는 임베딩 방법.
특징적인거는 매니폴드 학습(manifold learning)을 사용하는데, 매니폴드란 고차원 데이터가 있을 때 고차원 데이터를 데이터 공간에 뿌리면 샘플들을 잘 아우르는 Subspace가 있을 것이라 가정에서 학습을 진행하는 방법이다.
MDS: Multi-Dimensional Scaling, 다차원 척도법이라 하며, 1964년에 제안된 오래된 임베딩 방법이다.
D-차원 공간 상의 객체들이 있을 때 그 객체들의 거리(between object distance)가 저차원 공간 상에도 최대한 많이 보존되도록 하는 좌표계를 찾는 것을 의미한다.

사실 설명만 봐서는 잘 모르겠고, 진행하면서 이미지와 함께 살펴보기로 하자
목표
- MNIST 데이터셋을 훈련 세트와 테스트 세트로 분할
- t-SNE, PCA, LLE, MDS 등의 차원축소 알고리즘을 적용하여 2차원 데이터셋으로 변환
- 변환된 데이터셋에 대해 SVC, 랜덤포레스트 등의 분류기 학습
- 각 분류기의 성능 평가
- 추가: 3차원으로 차원축소를 진행한 결과와 비교
1. 원본 데이터셋 - 랜덤포레스트, SVC 분류기 학습 및 성능 평가
MNIST 데이터셋을 훈련 세트, 테스트 세트로 X, y 별 각 10,000개로 나눈다.
ps. 훈련 세트도 10,000개인 이유는 모델 훈련이 너무 오래 걸려서입니다.
# 데이터 로드
from sklearn.datasets import fetch_openml
mnist = fetch_openml('mnist_784',version=1)
mnist.target = mnist.target.astype(np.int)
X_train = mnist['data'][:10000]
y_train = mnist['target'][:10000]
X_test = mnist['data'][10000:20000]
y_test = mnist['target'][10000:20000]
사이킷런을 이용하여 랜덤 포레스트 모델 생성
- n_estimators=100, random_state=42 설정
from sklearn.ensemble import RandomForestClassifier
rnd_clf = RandomForestClassifier(n_estimators=100, random_state=42)
원본 데이터셋 - 랜덤 포레스트 모델 훈련
- time을 import 해서 훈련 시간 체크
import time
t0 = time.time()
rnd_clf.fit(X_train, y_train)
t1 = time.time()
print("훈련 시간 {:.2f}s".format(t1 - t0))
훈련 시간 6.21s
원본 데이터셋 - 랜덤 포레스트 정확성 평가
# 평가
from sklearn.metrics import accuracy_score
y_pred = rnd_clf.predict(X_test)
accuracy_score(y_test, y_pred)
0.9456
원본 데이터셋 - SVC 분류기 훈련
from sklearn.svm import LinearSVC
svc_clf = LinearSVC(C=1, random_state=24)
t0 = time.time()
svc_clf.fit(X_train,y_train)
t1 = time.time()
print("훈련 시간 {:.2f}s".format(t1 - t0))
훈련 시간 9.26s
원본 데이터셋 - SVC 정확성 평가
y_pred = svc_clf.predict(X_test)
accuracy_score(y_test,y_pred)
0.8572
1.1. t-SNE, PCA, LLE, MDS 차원축소 알고리즘 적용 - 2차원 데이터셋 변환
1.1.0. 데이터 및 그래프 설정
- 데이터셋은 10,000개를 가져온다.
- 그래프를 잘 그리기 위한 plot_digits 함수
mnist.target = mnist.target.astype(np.int)
np.random.seed(42)
m = 10000
idx = np.random.permutation(60000)[:m]
X = mnist['data'][idx]
y = mnist['target'][idx]
# 그래프 잘그리게 하는 코드
from sklearn.preprocessing import MinMaxScaler
from matplotlib.offsetbox import AnnotationBbox, OffsetImage
def plot_digits(X, y, min_distance=0.05, images=None, figsize=(13, 10)):
X_normalized = MinMaxScaler().fit_transform(X)
neighbors = np.array([[10., 10.]])
plt.figure(figsize=figsize)
cmap = mpl.cm.get_cmap("jet")
digits = np.unique(y)
for digit in digits:
plt.scatter(X_normalized[y == digit, 0], X_normalized[y == digit, 1], c=[cmap(digit / 9)])
plt.axis("off")
ax = plt.gcf().gca()
for index, image_coord in enumerate(X_normalized):
closest_distance = np.linalg.norm(np.array(neighbors) - image_coord, axis=1).min()
if closest_distance > min_distance:
neighbors = np.r_[neighbors, [image_coord]]
if images is None:
plt.text(image_coord[0], image_coord[1], str(int(y[index])),
color=cmap(y[index] / 9), fontdict={"weight": "bold", "size": 16})
else:
image = images[index].reshape(28, 28)
imagebox = AnnotationBbox(OffsetImage(image, cmap="binary"), image_coord)
ax.add_artist(imagebox)
1.1.1. t-SNE
t-SNE 차원 축소 그래프
- X, y 기준
from sklearn.manifold import TSNE
t0 = time.time()
X_tsne_reduced = TSNE(n_components=2, random_state=42).fit_transform(X)
t1 = time.time()
print("t-SNE 훈련 시간: {:.1f}s.".format(t1 - t0))
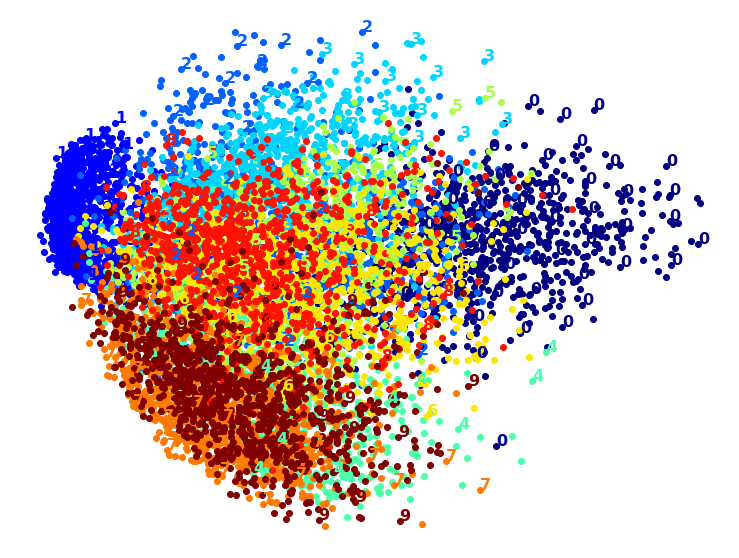
plot_digits(X_tsne_reduced, y)
plt.show()
t-SNE 훈련 시간: 270.8s.

t-SNE 차원 축소 그래프
- X_test, y_test 기준
X_tsne_test = TSNE(n_components=2, random_state=42).fit_transform(X_test)
plot_digits(X_tsne_test, y_test)
plt.show()

1.1.2. PCA
PCA 차원 축소 그래프
- X, y 기준
from sklearn.decomposition import PCA
import time
t0 = time.time()
X_pca_reduced = PCA(n_components=2, random_state=42).fit_transform(X)
t1 = time.time()
print("PCA 훈련 시간 {:.1f}s.".format(t1 - t0))
plot_digits(X_pca_reduced, y)
plt.show()
PCA 훈련 시간 0.9s.

PCA 차원 축소 그래프
- X_test, y_test 기준
X_pca_test = PCA(n_components=2, random_state=42).fit_transform(X_test)
plot_digits(X_pca_test, y_test)
plt.show()
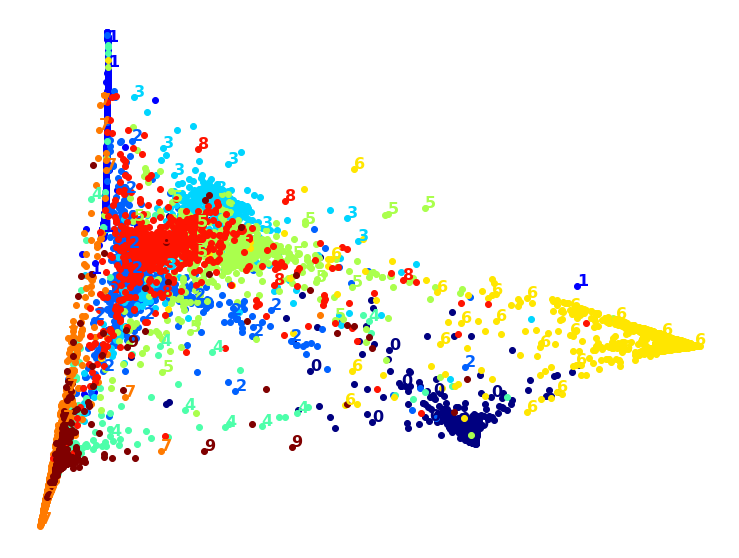
1.1.3. LLE
LLE 차원 축소 그래프
- X, y 기준
from sklearn.manifold import LocallyLinearEmbedding
t0 = time.time()
X_lle_reduced = LocallyLinearEmbedding(n_components=2, random_state=42).fit_transform(X)
t1 = time.time()
print("LLE 훈련 시간 {:.1f}s.".format(t1 - t0))
plot_digits(X_lle_reduced, y)
plt.show()
LLE 훈련 시간 195.7s.
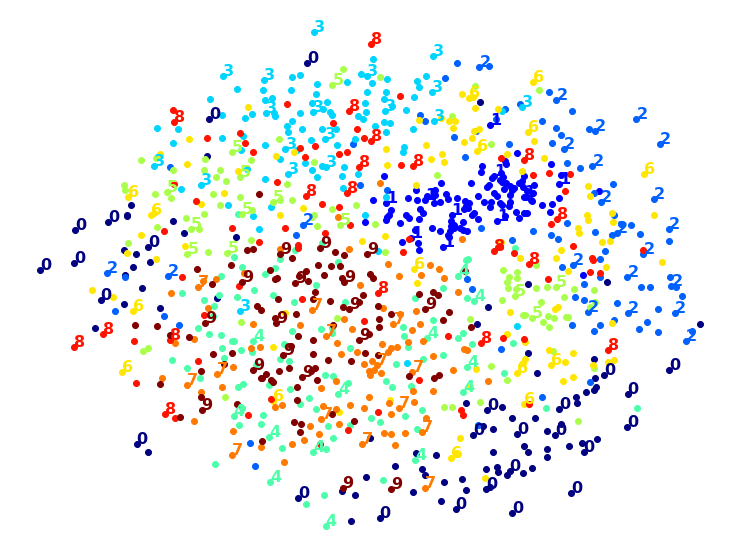
LLE 차원 축소 그래프
- X_test, y_test 기준
X_lle_test = LocallyLinearEmbedding(n_components=2, random_state=42).fit_transform(X_test)
plot_digits(X_lle_test, y_test)
plt.show()

1.1.4. MDS
MDS 차원 축소 그래프
- X, y 기준
- 다른 차원축소보다 시간이 오래걸리기 때문에 m = 1,000 기준으로 실행
from sklearn.manifold import MDS
m = 1000
t0 = time.time()
X_mds_reduced = MDS(n_components=2, random_state=42).fit_transform(X[:m])
t1 = time.time()
print("MDS 훈련 시간 {:.1f}s".format(t1 - t0))
plot_digits(X_mds_reduced, y[:m])
plt.show()
MDS 훈련 시간 37.4s

MDS 차원 축소 그래프
- X_test, y_test 기준
- 다른 차원축소보다 시간이 오래걸리기 때문에 m = 1,000 기준으로 실행
X_mds_test = MDS(n_components=2, random_state=42).fit_transform(X_test[:m])
plot_digits(X_mds_test, y_test[:m])
plt.show()
1.2. 2차원 변환 데이터셋 - 랜덤포레스트, SVC 분류기 학습 및 성능 평가
변환 데이터셋 - 랜덤 포레스트 모델 훈련 및 정확성 평가
# 랜덤 포레스트 평가
rnd_clf2 = RandomForestClassifier(n_estimators=100,random_state=42)
# t-SNE
rnd_clf2.fit(X_tsne_reduced, y)
y_pred = rnd_clf2.predict(X_tsne_test)
acsc_tsne = accuracy_score(y_test, y_pred)
# PCA
rnd_clf2.fit(X_pca_reduced, y)
y_pred = rnd_clf2.predict(X_pca_test)
acsc_pca = accuracy_score(y_test, y_pred)
# LLE
rnd_clf2.fit(X_lle_reduced, y)
y_pred = rnd_clf2.predict(X_lle_test)
acsc_lle = accuracy_score(y_test, y_pred)
# MDS
rnd_clf2.fit(X_mds_reduced, y[:m])
y_pred = rnd_clf2.predict(X_mds_test)
acsc_mds = accuracy_score(y_test[:m], y_pred)
print(acsc_tsne, acsc_pca, acsc_lle, acsc_mds)
0.1298 0.1198 0.3171 0.145
정확성 평가 값이 그렇게 높게 나오진 않는다.
변환 데이터셋 - SVC 분류기 훈련 및 정확성 평가
# SVC 분류기 평가
from sklearn.svm import LinearSVC
svc_clf2 = LinearSVC(C=1, random_state=42)
# t-SNE
svc_clf2.fit(X_tsne_reduced, y)
y_pred = svc_clf2.predict(X_tsne_test)
acsc2_tsne = accuracy_score(y_test, y_pred)
# PCA
svc_clf2.fit(X_pca_reduced, y)
y_pred = svc_clf2.predict(X_pca_test)
acsc2_pca = accuracy_score(y_test, y_pred)
# LLE
svc_clf2.fit(X_lle_reduced, y)
y_pred = svc_clf2.predict(X_lle_test)
acsc2_lle = accuracy_score(y_test, y_pred)
# MDS
svc_clf2.fit(X_mds_reduced, y[:m])
y_pred = svc_clf2.predict(X_mds_test)
acsc2_mds = accuracy_score(y_test[:m], y_pred)
print(acsc2_tsne, acsc2_pca, acsc2_lle, acsc2_mds)
0.1438 0.1015 0.1739 0.11
얘도 정확성 평가 값이 그렇게 높게 나오진 않는다.
1.3 t-SNE, PCA, LLE, MDS 차원축소 알고리즘 적용 - 3차원 데이터셋 변환
- 데이터셋 설정은 위의 2차원 변환에서 이미 불러왔다.
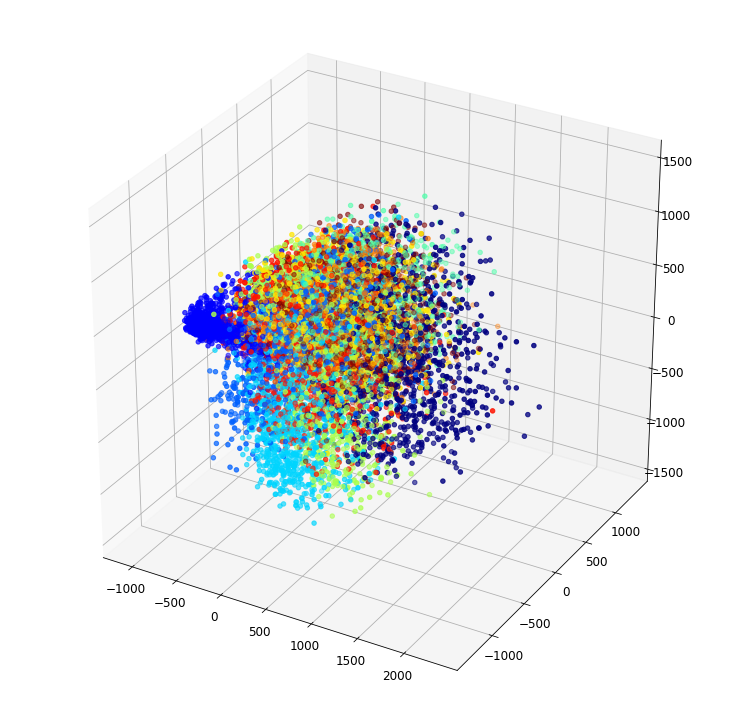
1.3.1. t-SNE
from sklearn.manifold import TSNE
t0 = time.time()
X3_tsne_reduced = TSNE(n_components=3, random_state=42).fit_transform(X)
t1 = time.time()
print("t-SNE 훈련 시간: {:.1f}s.".format(t1 - t0))
plt.rcParams["figure.figsize"] = (13, 13)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(X3_tsne_reduced[:, 0],X3_tsne_reduced[:, 1],X3_tsne_reduced[:, 2], c=y, cmap='jet' )
plt.show()
t-SNE 훈련 시간: 614.0s.

1.3.2. PCA
from sklearn.decomposition import PCA
import time
from mpl_toolkits.mplot3d import Axes3D
t0 = time.time()
X3_pca_reduced = PCA(n_components=3, random_state=42).fit_transform(X)
t1 = time.time()
print("PCA 훈련 시간 {:.1f}s.".format(t1 - t0))
plt.rcParams["figure.figsize"] = (13, 13)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(X3_pca_reduced[:, 0],X3_pca_reduced[:, 1],X3_pca_reduced[:, 2], c=y, cmap='jet' )
plt.show()
PCA 훈련 시간 1.0s.
1.3.3. LLE
from sklearn.manifold import LocallyLinearEmbedding
t0 = time.time()
X3_lle_reduced = LocallyLinearEmbedding(n_components=3, random_state=42).fit_transform(X)
t1 = time.time()
print("LLE 훈련 시간 {:.1f}s.".format(t1 - t0))
plt.rcParams["figure.figsize"] = (13, 13)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(X3_lle_reduced[:, 0],X3_lle_reduced[:, 1],X3_lle_reduced[:, 2], c=y, cmap='jet' )
plt.show()
LLE 훈련 시간 194.3s.

1.3.4. MDS
from sklearn.manifold import MDS
m = 1000
t0 = time.time()
X3_mds_reduced = MDS(n_components=3, random_state=42).fit_transform(X[:m])
t1 = time.time()
print("MDS 훈련 시간 {:.1f}s".format(t1 - t0))
plt.rcParams["figure.figsize"] = (13, 13)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(X3_mds_reduced[:, 0],X3_mds_reduced[:, 1],X3_mds_reduced[:, 2], c=y[:m], cmap='jet' )
plt.show()
MDS 훈련 시간 35.3s

1.4. 3차원 변환 데이터셋 - 랜덤포레스트, SVC 분류기 학습 및 성능 평가
변환 데이터셋 - 랜덤 포레스트 모델 훈련 및 정확성 평가
# 랜덤 포레스트 평가
rnd_clf3 = RandomForestClassifier(n_estimators=100,random_state=42)
X3_tsne_test = PCA(n_components=3, random_state=42).fit_transform(X_test)
X3_pca_test = PCA(n_components=3, random_state=42).fit_transform(X_test)
X3_lle_test = PCA(n_components=3, random_state=42).fit_transform(X_test)
X3_mds_test = PCA(n_components=3, random_state=42).fit_transform(X_test[:m])
# t-SNE
rnd_clf3.fit(X3_tsne_reduced, y)
y_pred = rnd_clf3.predict(X3_tsne_test)
acsc_tsne3 = accuracy_score(y_test, y_pred)
# PCA
rnd_clf3.fit(X3_pca_reduced, y)
y_pred = rnd_clf3.predict(X3_pca_test)
acsc_pca3 = accuracy_score(y_test, y_pred)
# LLE
rnd_clf3.fit(X3_lle_reduced, y)
y_pred = rnd_clf3.predict(X3_lle_test)
acsc_lle3 = accuracy_score(y_test, y_pred)
# MDS
rnd_clf3.fit(X3_mds_reduced, y[:m])
y_pred = rnd_clf3.predict(X3_mds_test)
acsc_mds3 = accuracy_score(y_test[:m], y_pred)
print(acsc_tsne3, acsc_pca3, acsc_lle3, acsc_mds3)
0.0855 0.1415 0.1594 0.126
변환 데이터셋 - SVC 분류기 훈련 및 정확성 평가
# SVC 분류기 평가
from sklearn.svm import LinearSVC
svc_clf3 = LinearSVC(C=1, random_state=42)
# t-SNE
svc_clf3.fit(X3_tsne_reduced, y)
y_pred = svc_clf3.predict(X3_tsne_test)
acsc2_tsne3 = accuracy_score(y_test, y_pred)
# PCA
svc_clf3.fit(X3_pca_reduced, y)
y_pred = svc_clf3.predict(X3_pca_test)
acsc2_pca3 = accuracy_score(y_test, y_pred)
# LLE
svc_clf3.fit(X3_lle_reduced, y)
y_pred = svc_clf3.predict(X3_lle_test)
acsc2_lle3 = accuracy_score(y_test, y_pred)
# MDS
svc_clf3.fit(X3_mds_reduced, y[:m])
y_pred = svc_clf3.predict(X3_mds_test)
acsc2_mds3 = accuracy_score(y_test[:m], y_pred)
print(acsc2_tsne3, acsc2_pca3, acsc2_lle3, acsc2_mds3)
0.0611 0.1115 0.2475 0.198
1.5. 2차원, 3차원 데이터셋 성능 평가 비교
2차원 변환 데이터셋
- t-SNE PCA LLE MDS
- rnd: 0.1298 0.1198 0.3171 0.145
- svc: 0.1438 0.1015 0.1739 0.110
3차원 변환 데이터셋
- t-SNE PCA LLE MDS
- rnd: 0.0855 0.1415 0.1594 0.126
- svc: 0.0611 0.1115 0.2475 0.198
2차원 변환 데이터셋
- 2차원 변환 데이터셋에서 LLE 모델이 성능 평가 시 가장 좋은 성능을 보여주었다.
- t-SNE 차원축소 데이터를 제외하고 랜덤포레스트보다 SVC가 비교적 성능이 좋지 않았다.
3차원 변환 데이터셋
- 3차원 변환 데이터셋에서도 LLE 모델이 성능 평가 시 가장 좋은 성능을 보여주었다.
- 성능 평가를 비교하였을 때 t-SNE, PCA는 랜덤포레스트가 LLE, MDS는 SVC가 성능 평가가 좋게 나왔다.
2차원과 3차원 변환 데이터셋 비교
- PCA는 3차원 데이터가 평가 시 성능이 좋게 나왔다. 반대로 t-SNE는 2차원 데이터가 평가 시 성능이 좋았다.
- LLE와 MDS는 특이하게도 랜덤포레스트는 2차원이 SVC는 3차원 데이터셋이 성능이 좋게 나왔다.
요약
MNIST 데이터셋과 2차원 t-SNE, PCA, LLE, MDS 학습
- MNIST 데이터셋에서 10,000개의 데이터만 가져온다.
그리고 t-SNE, PCA, LLE, MDS을 이용하여 2차원으로 축소시킨다. - MDS 차원 축소같은 경우 다른 차원축소보다 시간이 오래걸려서 1,000개로 나누었다.
- 변환한 데이터셋을 랜덤 포레스트와 SVC 분류기로 학습하고 성능을 평가하였다.
MNIST 데이터셋과 3차원 t-SNE, PCA, LLE, MDS 학습
- 마찬가지로 MNIST 데이터셋에서 10,000개의 데이터만 가져온다.
그리고 t-SNE, PCA, LLE, MDS을 이용하여 3차원으로 변환시킨다.
MDS 차원 축소같은 경우 다른 차원축소보다 시간이 오래걸려서 1,000개로 나누었다. - 변환한 데이터셋을 랜덤 포레스트와 SVC 분류기로 학습하고 성능을 평가하였다.
2차원, 3차원 모델 성능 평가 비교
- 2차원 변환 데이터셋
- 2차원 변환 데이터셋에서 LLE 모델이 성능 평가 시 가장 좋은 성능을 보여주었다.
t-SNE 차원축소 데이터를 제외하고 랜덤포레스트보다 SVC가 비교적 성능이 좋지 않았다.
- 2차원 변환 데이터셋에서 LLE 모델이 성능 평가 시 가장 좋은 성능을 보여주었다.
- 3차원 변환 데이터셋
- 3차원 변환 데이터셋에서도 LLE 모델이 성능 평가 시 가장 좋은 성능을 보여주었다.
성능 평가를 비교하였을 때 t-SNE, PCA는 랜덤포레스트가 LLE, MDS는 SVC가 성능 평가가 좋게 나왔다.
- 3차원 변환 데이터셋에서도 LLE 모델이 성능 평가 시 가장 좋은 성능을 보여주었다.
- 2차원과 3차원 변환 데이터셋 비교
- PCA는 3차원 데이터가 평가 시 성능이 좋게 나왔다.
반대로 t-SNE는 2차원 데이터가 평가 시 성능이 좋았다.
LLE와 MDS는 특이하게도 랜덤포레스트는 2차원이 SVC는 3차원 데이터셋이 성능이 좋게 나왔다.
- PCA는 3차원 데이터가 평가 시 성능이 좋게 나왔다.
- 참고 문헌: 핸즈온 머신러닝
- Github link: 머신러닝 실습 7
